§7.5 曲面及其方程

一 曲面方程的概念

空间曲面可看做点的轨迹，而点的轨迹可由点的坐标所满足的方程来表达。因此，空间曲面可由方程来表示，反过来也成立。

为此，我们给出如下定义：

若曲面与三元方程

(1)

有下述关系：

1、曲面上任一点的坐标均满足方程(1)；

2、不在曲面上的点的坐标都不满足方程(1)。

那么，方程(1)称作曲面的方程，而曲面称作方程(1)的图形。

下面，我们来建立几个常见的曲面方程。

【例1】 球心在点，半径为的球面方程。

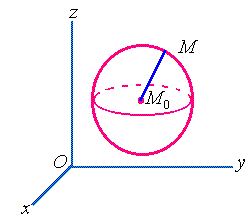
解：设是球面上的任一点，那么，

即：

(2)

(2)式就是球面上任一点的坐标所满足的方程。

反过来，不在球面上的点，到的距离， 从而点的坐标不适合于方程(2)。

故方程(2)就是以为球心，为半径的球面方程。

若球心在原点，即，其球面方程为

【例2】设有点和，求线段垂直平分面的方程。

解：所求平面是与和等距离的点的几何轨迹，设是所求平面上任意的一点，则

即：

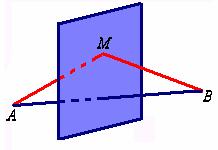
化简得

这便是平面的方程。

上述两例告诉我们如下事实：

作为点的几何轨迹的曲面可以用它的坐标间的方程来表示，反过来，变量之间的方程一般地表示点的轨迹所形成的曲面。

因此，空间解析几何关于曲面的研究，有以下两个基本问题：

第一、已知曲面作为点的几何轨迹，建立该曲面的方程；

第二、已知坐标的方程，研究该方程所表示的曲面形状。

二 旋转曲面

先看一个特殊的旋转曲面。

【例3】设有一条过原点，且与轴夹角为的直线，求直线绕轴旋转所产生的曲面的方程。(绕轴旋转时，始终与轴保持定角)

解：设开始位于平面，是上一点，则

当转动时，点转到点在的转动过程中，点的竖坐标满足

且点到轴的距离满足

从而

或 (3)

其中 。

这表明：曲面上任一点的坐标一定满足方程(3)；反过来，如果不在曲面上，那么直线与轴的夹角就不等于，于是，点的坐标就不满足方程(3)。因此，方程(3)便是所求的曲面方程。

上述曲面称之为圆锥面，动直线与轴的交点称之为圆锥面的顶点，定角称为圆锥面的半顶角。

一般地，我们给出旋转曲面的定义如下：

一条平面曲线绕其平面上的一条定直线旋转一周所成的曲面叫做旋转曲面，这条定直线叫做旋转曲面的轴。

显然，圆锥面是一种旋转曲面，求平面上的直线绕轴旋转所成的圆维面，只需将改成，即可得到圆锥面的方程

用类似的方法，可求出一般旋转曲面的方程。

设在平面上有一条已知曲线，它的方程为 ,将绕轴旋转一周，得到以轴为轴的旋转曲面。

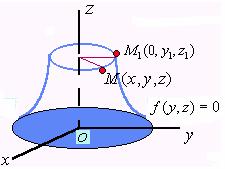
设是上任一点的坐标，则 ,当点旋转到点时，总有

点到轴的距离为

将， 代入方程得到

这便是所要求的旋转曲面的方程。

同理，曲线 绕 轴旋转所成的旋转曲面方程为

【例4】将面上的双曲线

分别绕 轴或轴旋转一周， 求所生成的旋转曲面的方程

解：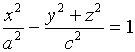

或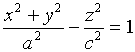

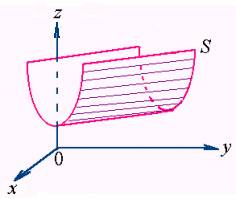
三 柱面

先分析一个实例

【例5】方程表示怎样的曲面?

解：在面上表示圆心在原点，半径为的圆。

在空间直角坐标中，该方程不含变量，即不论取何值，只要横坐标和纵坐标适合方程的空间点均在该曲面上。也就是说，过圆上的点且平行于轴的直线都在该曲面上。

因此，曲面是由平行于轴的直线沿面上的圆移动而形成的。

这一曲面称作圆柱面。面上的圆称之为准线，那些平行于轴且过准线的直线叫做母线。

一般地，我们给出柱面的定义如下：

平行于定直线并沿定曲线移动的直线形成的轨迹称之为柱面。 定曲线称为柱面的准线， 动直线称为柱面的母线。

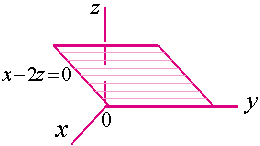
【例6】指出下列曲面是否为柱面， 并画出它们的图形。

(1) (2)

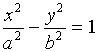(3) (4)

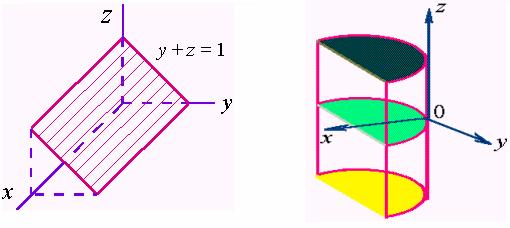
解：(1)、曲面可看作：以面上的直线为准线，以平行于轴的直线为母线而形成的柱面(平面)。

(2)、曲面表示母线平行于轴，以面上的曲线为准线的抛物柱面。

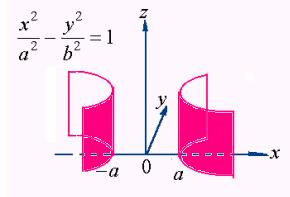
(3)、该曲面方程中缺少变量，故它表示母线平行于轴，而准线为面上曲线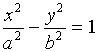所形成的双曲柱面。

(4)、该曲面方程中缺少变量，故它表示母线平行于轴，而准线为面上的曲线所形成的柱面(平面)